Day 7 of 10: Ingressive For Good Data Structures and Algorithm Challenge

The second half of this challenge is definitely not for the weak. We went from easy to medium. and today i learnt about bitwise operators.

Instructions

Given an integer array data representing the data, return whether it is a valid UTF-8 encoding (i.e. it translates to a sequence of valid UTF-8 encoded characters).

A character in UTF8 can be from 1 to 4 bytes long, subjected to the following rules:

For a 1-byte character, the first bit is a 0, followed by its Unicode code. For an n-bytes character, the first n bits are all one's, the n + 1 bit is 0, followed by n - 1 bytes with the most significant 2 bits being 10. This is how the UTF-8 encoding would work:

     Number of Bytes   |        UTF-8 Octet Sequence
                       |              (binary)
   --------------------+-----------------------------------------
            1          |   0xxxxxxx
            2          |   110xxxxx 10xxxxxx
            3          |   1110xxxx 10xxxxxx 10xxxxxx
            4          |   11110xxx 10xxxxxx 10xxxxxx 10xxxxxx

x denotes a bit in the binary form of a byte that may be either 0 or 1.

Note: The input is an array of integers. Only the least significant 8 bits of each integer is used to store the data. This means each integer represents only 1 byte of data.

Testcase

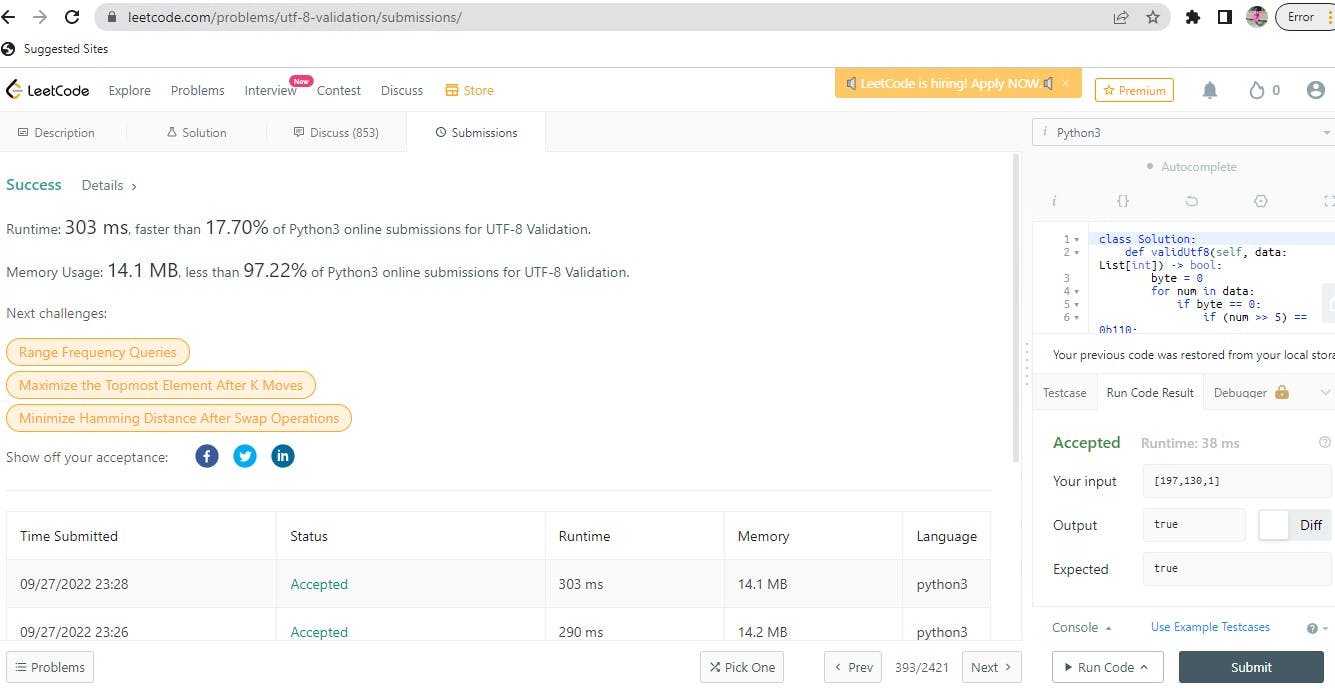
Input: data = [197,130,1]
Output: true

Explanation: data represents the octet sequence: 11000101 10000010 00000001. It is a valid utf-8 encoding for a 2-bytes character followed by a 1-byte character.

My Solution

First of all, i defined a variable byte to store the number of bytes of the binary equivalent and initialised as zero.

Then for, each number in the array given, i used the bitwise operator >> to specify the following conditions:

1. If the binary equivalent of the number when shifted to the right five times(i.e x >> 5, this eliminates the last five digits) gives the first three digits as 110 in the form "0b110", then it is a 2-byte number and thus, utf-8 encoded.

2. If the binary equivalent of the number when shifted to the right four times(i.e x >> 4, this eliminates the last four digits) gives the first four digits as 1110 in the form "0b1110", then it is a 3-byte number and thus, utf-8 encoded.

3. If the binary equivalent of the number when shifted to the right three times(i.e x >> 3, this eliminates the last three digits) gives the first five digits as 11110 in the form "0b11110", then it is a 4-byte number and thus, utf-8 encoded.

4. If all conditions above fail but the binary equivalent of the number when shifted to the right seven times(i.e x >> 7, this eliminates the last six digits) yields a digit then it is not utf-8 encoded.

5 If If all conditions above fail and the binary equivalent of the number doesnt start with 10(i.e x>>6 != 0b10), then it is not utf-8 encoded.

This produced a memory usage of 14mb but after running for the second and third time, it increased by .1mb.

You can view my submission details below.